Les fentes en optique
Introduction
Pour les astronomes amateurs le premier usage de la fente est l’appareil de Foucault.
J. Texerau, dans son livre La construction du télescope d’amateur (voir la bibliothèque) indique en préambule (page 53 chap.30) que les résultats sont optimaux pour une fente de 8 à 10 µm de l’ordre du diamètre de la tache de diffraction au centre de courbure. Et pour les miroirs dont il est question (200 mm ouverts entre 6 et 8) cette tache est de 8 et 10 µm. Le seul bémol à ces prescriptions de largeur de sources est une petite phrase (page 53) qui s’étonne que la méthode marche encore avec une fente 10 fois plus grande (ça reste donc en dessous de 100µm) pour les contrôles courants (cela semble exclure la mesure finale de la parabolisation). Plus loin il conseille de réaliser une fente de 30 à 50 µm (page 55 chap.30 et 58 59 chap.32) pour suivre le travail de l’opticien par exemple en regardant la forme générales au Foucault sans masque (page 49 chap.28). Enfin il précise qu’il faut une fente de 10 à 20 µm lors de la parabolisation et pour le contrôle du miroir avec le masque de Couder (page 66 chap 39).
De nos jours, lorsque l’on taille son miroir, on peut se demander s’il ne faut pas une fente plus fine. Car les miroirs actuels font plus de 250 mm de diamètre et sont ouverts en dessous de 5. Ces miroirs donnent une image de diffraction au Foucault plus petite que celle des miroirs ouverts à 6 ou 8.
On comprend bien que si la fente est plus large que la taille de l’image de diffraction, son image au Foucault sera plus large que le minimum possible lié à la diffration. Et donc la plage de teinte grise sera plus étendue sur l’image sans écran et plus longue à traverser pour le couteau avec l’écran de Couder.
Car la mesure au Foucault avec écran de Couder fonctionne sur la perception du noircissement simultané des ouvertures diamétralement opposées de l’écran de Couder. Chacun fait l’expérience que la lenteur ne permet pas à l’œil de décider de la simultanéité du noircissement sur les deux zones. Élargir la zone de teinte grise peut donc avoir plus ou moins d’effet selon que la vis de manœuvre permet la dynamique appropriée. Mais si c’était toujours vrai, J. Texerau n’aurait-il pas pris soin de préciser ces choses.
De plus si on utilise le robot Foucault, tant le modèle simple avec une caméra et des masques posés sur l’écran télé, que celui plus élaboré avec une analyse automatisée des images, l’étalement de l’image de diffraction va correspondre à un étalement des zones grises. Ce qui conduit à moins bien discerner les positions du couteau ou le rayon sur le miroir. On augmente donc les aléas de la mesure.
Lorsque l’on croise ces considérations avec le fait que l’aberration de sphéricité des miroirs très ouverts actuels est une difficulté supplémentaire de mesure au Foucault, on se range vite à l’avis qu’il est prudent de disposer d’une fente de finesse appropriée. Se pose alors le problème de trouver la bonne largeur et de vérifier la largeur réalisée.
Voyons déjà comment mesurer la largeur d’une fente, car ce n’est pas avec un microscope ni avec un oculaire grossissant que l’on dispose d’une métrologie même approximative de ce genre d’objet.
Principes optiques
C’est en 1801 que Thomas Young découvre et interprète convenablement les interférences lumineuses. Elles sont alors obtenues avec deux trous éclairés par une source ponctuelle. L’expérience gagne en luminosité en remplaçant les deux trous par deux fentes. De même, lorsque la source est remplacée par une fente fine parallèle aux deux autres.
Depuis cette date, il est très courant d’utiliser des fentes comme source lumineuse en optique. L’intérêt de la fente réside dans sa facilité de fabrication par rapport à un trou de même largeur et dans sa forte luminosité toujours par rapport à un trou. Son inconvénient est qu’il faut tolérer une source lumineuse étendue selon une direction de l’espace.
L’interférence est le résultat de l’interaction de deux ondes (ou d’un petit nombre d’ondes). Pour Young c’est deux ondes passant par deux trous ou deux fentes. La diffraction, elle, traite du comportement d’une seule onde passant au travers d’une seule ouverture. Le phénomène de diffraction existe pour toutes les tailles d’ouverture et pour toutes les longueurs d’onde. Mais il est manifeste dès que la taille de l’ouverture se rapproche de la taille caractéristique de l’onde : Sa longueur d’onde.
Les longueurs des ondes visibles sont comprises entre 0,4 et 0,7 microns. On considère que l’œil en vision diurne est le plus sensible aux longueurs d’onde du vert au voisinage de 0,55 microns. Ainsi on peut observer à l’œil des phénomènes de diffraction sur la lumière visible pour une fente de quelques microns à quelques dizaines de microns. Avec un télescope, dont l’ouverture est décimétrique, on ne peut observer la diffraction qu’à condition de grossir fortement avec un oculaire ou un microscope.
Le phénomène de diffraction peut être interprété en termes d’interférences, non pas entre deux ondes mais, entre l’infinité des ondes élémentaires qui seraient logeables sur toute la largeur de la fente.
On note traditionnellement la largeur de la fente par a et lambda ou λ la longueur d’onde de la lumière.
En présence d’un phénomène de diffraction on constate que la lumière qui traverse une fente en venant d’une source lumineuse ne se dirige pas seulement selon l’axe source lumineuse – ouverture de la fente. Après la fente, la lumière est envoyée dans plusieurs directions. On dit qu’elle est diffractée. Elle est diffractée dans un angle approximativement égal à λ/a (en radians).
Plus précisément, un calcul intégral montre qu’une pupille rectangulaire de largeur a, éclairée par une onde plane monochromatique de longueur d’onde λ, donne à l’infini (dans la pratique : loin de la fente) une distribution angulaire d’amplitude variable selon une loi variant sinus cardinal de l’angle de diffraction :
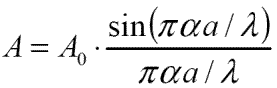
Avec A l’amplitude de l’onde et α l’angle par rapport à l’axe source-fente.
Ce qui donne une intensité lumineuse perçue à l’œil I variant avec le carré de ce sinus cardinal :
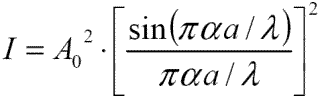
On calcul facilement que l’intensité lumineuse est nulle à chaque multiple entier Pi :
N.B. : Sauf pour zéro où le sinus cardinal est maximum et vaut 1. Ce qui donne le maximum de luminosité dans l’axe du système.
On s’intéresse usuellement de l’écart angulaire de la première frange sombre :
Et comme on mesure cet angle par projection sur un écran placé à une grande distance L, l’écart sur l’axe de la première frange sombre est donné pas :
On note immédiatement la similitude avec l’expression du rayon d’Airy :
Premier rayon sombre des images de diffraction au foyer des télescopes. Avec F la focale du télescope et D son diamètre. On a ici les mêmes éléments que L la distance de l’écran et a la largeur de l’ouverture de la fente.
Comment manipuler ?
Avec mesure !
Voir l’article sur les risques dans mon carnet d’humeurs. Personnellement, les manips sont toujours l’occasion de faire marcher les neurônes bien au-delà de la vitesse limite ce qui est très dangereux en plus d’être jalousé partout dans le monde (voir interdit en France…).
Commissions:
Une pièce noire de plus de 12 mètres carrées abritée des intempéries et ventilée, une table, un écran en papier blanc A3 (ou plus), un pointeur laser rouge ou vert, des Legos pour fixer la fente verticalement sur la table, un mètre ruban, du papier collant pour fixer tout ça et un crayon.
Mise en place :
Définissez la position du laser et de la fente pour être entre 150 et 200 cm d’un mur bien orthogonal. Préparez l’écran sur le mur centré sur l’axe du laser. Mettez la fente environs 10 cm devant le laser et fixez-la fermement en hauteur et en orientation. Vérifiez que la fente est bien orthogonale à l’axe du montage. Verrouillez le bouton de marche du laser et fixez-le sur la table. Le faisceau doit éclairer la fente… Il y a donc des réglages à faire avec des bouts de papiers et du collant.
Mise en conditions :
Vérifiez qu’il n’y a pas de risque de canicule. Se mettre dans le noir et prendre le temps d’admirer la démonstration de la nature ondulatoire de la lumière. Si vous n’avez rien d’autre à admirer qu’un point lumineux sur le mur; c’est que votre fente fait plusieurs centaines de microns de large ou que dans le volume de votre pièce les lois de la physique sont différentes de celles de la vulgate. Une fois bien imprégnée de la doctrine ondulante, vos pupilles seront assez dilatées pour voir les plus faibles lueurs de l’image de diffraction.
Manip :
Crayonnez sur la feuille les positions des franges noires. Attention, si la manip est mal mise en place, c’est la tapisserie qui paye. Et attention à la pointe du crayon manipulé dans le noir comme aux reflets du laser dans les lunettes… Rallumez pour éteindre le laser. Mesurez la distance entre le mur et la fente. Faites les calculs. Au besoin appliquez le principe de précaution: Faire les calculs après s’être lavé les cheveux pour pouvoir se gratter la tête sans risque de se salir les ongles.
Abaque pour les lasers rouge (650 nm) et vert (532 nm):
| Larguer de fente | Écartement des franges à un mètre à 650 nm | Écartement des franges à un mètre à 532 nm |
| [ µm ] | [ millimètre ] | [ millimètre ] |
| 5 | 131 | 107 |
| 10 | 65 | 53 |
| 15 | 43 | 35 |
| 20 | 33 | 27 |
| 30 | 22 | 18 |
| 40 | 16 | 13 |
| 50 | 13 | 11 |
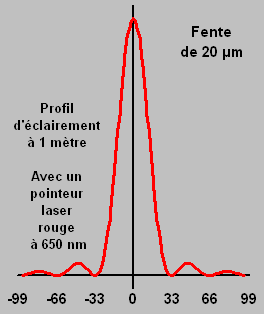
Les ambiguïtés de mesure: Il n’y a pas de frange sombre au centre. Certes évident après coup… Mais comme le montre le schéma, c’est bien du centre de la figure qu’il faut compter l’écartement. Et comme le centre est noyé dans la luminosité, il très difficile à trouver. Donc on mesure l’espacement des deux premières franges, les plus visibles, puis on divise par deux. Ensuite on vérifie l’écartement trouvé entre les franges d’ordre supérieur afin de détromper une erreur éventuelle. Pour repérer finement les premières franges sombres, il faut veiller à trouver le point de moindre éclairement. Or la forte croissance de la luminosité vers le centre de l’image peut tromper le cerveau qui se cache derrière l’œil. Il est alors bon de refaire la mesure en ayant masqué la zone centrale pour mieux apprécier les zones périphériques de faible luminosité. Enfin, si la largeur de la fente varie fortement du haut en bas, la figure de diffraction est la somme des figures pour chaque largeur et le minimum d’éclairement est noyé dans un fond diffus qui empêche de bien trouver le minimum. Il faut alors essayer de n’éclairer qu’un morceau de la fente
Résultats personnels
Fente réalisée avec deux morceaux de lame de cutters collés sur une plaquette d’aluminium perforée en 3 mm. Au Foucault on observe un léger défaut de parallélisme de la fente.
Laser vert à 532 nm. Distance fente-écran de 1730mm. Écran de papier blanc bien orthogonal à l’axe optique.
Premières franges sombres écartées de 100 mm (faciles à mesurer) et suivantes 50 mm plus loin mais plus difficiles à juger finement compte tenu de la baisse de luminosité. Les franges suivantes sont encore visibles mais très difficiles à mesurer. En reproduisant le montage plusieurs fois et en tâchant de viser tantôt le haut puis le bas de la fente qui s’étale sur 3 mm de haut, j’ai obtenu des valeurs variant entre 48 et 52.
Donc 0,532 fois 1,730 divisé par 50 donnent 0,0184 mm ou 18,4 µm.
La reproduction de l’essai avec un laser rouge à 650 nm éclairant toute la hauteur de la fente donne 18 µm en cohérence avec le laser vert. Simplement les franges sont moins lumineuses compte tenu de la puissance du laser et de la sensibilité spectrale de l’œil.
Compte tenu des divers aléas de mesure, j’ai une fente, sans aucun doute imparfaitement parallèle, mais comprise entre 17,5 et 19,5 µm.
J’ai donc bien une fente assez semblable par sa largeur à l’image de diffraction donnée par mes miroirs lors du test de Foucault : 1,22 x 0,55 x 1250 x 2 / 250 donnent 7 µm de rayon d’Airy pour mon 250 mm ouvert à 5 et 8 µm pour le petit dernier de 200 mm ouvert à 6. Donc des diamètres de taches de diffraction de 14 et 16 µm au mieux en pleine ouverture sans écran de Couder.
Ce qui donne l’envie de réaliser une fente de 10 µm et une de 40 µm pour voir la différence. Pour un prochain miroir peut-être…