Calcul des déformations du verre induites par les supports
Pierre Strock (http://strock.pi.r2.3.14159.free.fr)
12 août 2007
Introduction
Pendant des années l’astronome amateur a appliqué les trucs des anciens. Puis un jour, un ingénieur japonais du nom Toshimi TAKI à bousculé les vieux a priori à l’aide de quelques calculs aux éléments finis (in Sky & Telescope, April 1996, pp.75-77) (voir son site sur http://www.asahi-net.or.jp/~zs3t-tk/ ). Ceux que l’on utilise pour calculer les ponts et les immeubles. Il a abattu d’un coup le principe de Texereau consistant à supporter les miroirs sur trois points en périphérie et aussi celui des constructeurs de télescope consistant à mettre les points à 70% du rayon. Enfin un ingénieur canadien du nom de David LEWIS a développé un code de calcul aux éléments finis pour les amateurs : PLOP (voir son site sur http://www.davidlewistoronto.com/ ). Les astronomes ont alors pu faire ce que les professionnels faisaient depuis des années : optimiser l’épaisseur (donc le poids et le coût) du verre selon la difficulté de réaliser le barillet.
Les calculs avec PLOP sont indispensables pour définir le support optimum d’un miroir de petite taille. Je ne saurai que recommander de bien maîtriser cet outil.
Toutefois dans mes réflexions pour progresser vers un très gros télescope, j’avais besoin d’abaques ou de règles approchées et simples. Je ne souhaitais pas faire des calculs PLOP à tout bout de champ, d’autant plus que les structures avec beaucoup de points ne sont pas rapides à introduire dans le code.
J’ai donc recherché une formulation approchée permettant de sentir le comportement du miroir selon qu’on lui ajoute de l’épaisseur ou des points de support. J’ai mis au point une formule approchée de la déformation Pic-Vallée (usuellement désignée PV mais aussi crête-à-creux) du verre en considérant que le verre fléchit comme une poutre. Cette formulation s’est avérée fort juste en la comparant à des calculs PLOP.
Et puis un jour par hasard, je suis tombé sur quelques rares publications professionnelles qui traitaient de manière plus rigoureuse de ce problème et qui donnaient les déformations PV et rms du verre (rms pour « root mean square » en anglais ou « écart type » en français).
Muni de ces belles formules, il est intéressant d’en faire quelque chose. Le premier usage est éducatif. On appréhende mieux les facteurs intervenant dans la déformation du verre. Le second est divertissant. On peut vérifier le lambda induit par les supports des miroirs professionnels.
Approximation de la poutre
Idée de base
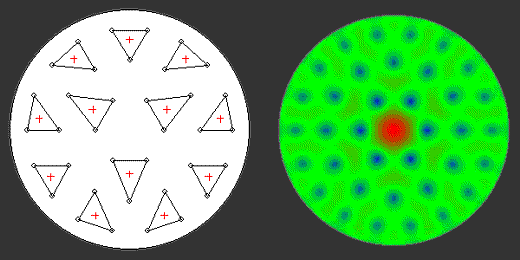
Sur un grand miroir avec de nombreux points d’appuis, on constate que les points sont régulièrement espacés. Ainsi chaque point supporte sensiblement la même surface et la même masse de verre. Entre deux points le verre plie sous son poids. D’aucuns objecteront qu’il ne faut pas se contenter de la ligne droite entre deux points mais aussi regarder au centre des mailles triangulaires ou carrées. Certes, mais avançons !
Des formules simples de résistances des matériaux (RdM comme on disait en classe) permettent de calculer la flèche qu’aurait une poutre de verre entre deux points d’appuis. Ceux qui ont quelques notions de RdM objecteront bien que la formule fait l’impasse sur la liaison entre poutres et sur les effets latéraux. Certes la plaque de verre ne ressemble pas à une poutre !
Mais voyons déjà ce que donne un calcul simple de flexion de poutre par rapport à un calcul rigoureux avec PLOP. Prenons le risque que cela marche !
Idée de base
Sur un grand miroir avec de nombreux points d’appuis, on constate que les points sont régulièrement espacés. Ainsi chaque point supporte sensiblement la même surface et la même masse de verre. Entre deux points le verre plie sous son poids. D’aucuns objecteront qu’il ne faut pas se contenter de la ligne droite entre deux points mais aussi regarder au centre des mailles triangulaires ou carrées. Certes, mais avançons !
Des formules simples de résistances des matériaux (RdM comme on disait en classe) permettent de calculer la flèche qu’aurait une poutre de verre entre deux points d’appuis. Ceux qui ont quelques notions de RdM objecteront bien que la formule fait l’impasse sur la liaison entre poutres et sur les effets latéraux. Certes la plaque de verre ne ressemble pas à une poutre !
Mais voyons déjà ce que donne un calcul simple de flexion de poutre par rapport à un calcul rigoureux avec PLOP. Prenons le risque que cela marche !
Formules
Distance entre points :
Pour un miroir d’aire A supporté par de nombreux points. Disons: n points. Chacun supporte une surface A/n . Je ne rentre pas dans le détail de la forme du maillage. Si le maillage est carré, la largeur de la maille est : l² = A/n . Si la maille est triangulaire, la largeur est : 0,866 . l² = A/n . L’écart entre les deux mailles est faible (7,5%).
Remarque anodine :
La qualité de l’image transmise par un miroir est essentiellement liée à l’amplitude des défauts. Mais un paramètre secondaire joue aussi : La longueur de corrélation des défauts. Tel que j’ai compris la chose, un miroir avec un défaut périodique s’apparente plus à un réseau de diffraction qu’à une miroir grossissant. Or un support maillé avec de nombreux points présente une longueur de corrélation.
Didier Levavasseur a explicité dans ses publications qu’il faut éviter les longueurs de corrélation en dessous du dixième du diamètre. La taille caractéristique de la maille atteint cette limite dès que l’on a plus de 79 points en maillage carré. Les miroirs à très grand nombre de points doivent donc avoir une amplitude de défaut très faible pour que ce paramètre secondaire ne détruise pas la qualité de l’image. Si les défauts sont de très faible amplitude, ils peuvent bien être périodiques !
Le pire étant d’avoir une défaut voisin de quatre centième du diamètre qui correspond à environ 400 points support. Les miroirs du VLT en ont 450…
Flèche de la poutre :
Sachant que je fais l’impasse sur les fixations aux extrémités sur les autres poutres voisines. La formule de RdM de la flèche d’une poutre de longueur l , avec une charge linéaire q et un module d’élasticité E est donné par :
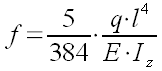
Sachant que la poutre n’est pas la plaque. Sachant que le moment d’inertie Iz d’une poutre de largeur b et d’épaisseur e est donnée par :
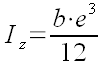
Je considère un miroir regardant au zénith. La charge linéaire q se calcule avec la masse volumique rho et l’accélération de la pesanteur g=9,81 m/s² par :
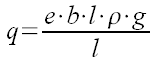
On arrive après simplification et pour une maille carrée la formule de la flèche du verre :
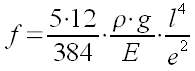
Premiers résultats :
Cette formule a déjà un intérêt. Elle permet de comprendre l’effet relatif de l’épaisseur du verre et du barillet sur la flèche. On sait ce qui influe sur la déformation Pic-Vallée du verre.
Ainsi si l’on complexifie un barillet en augmentant d’un facteur trois le nombre de ses points –c’est typiquement ce qui se passe lorsque l’on ajoute un triangle sur chaque point d’un support existant– les efforts repris par chaque point sont divisés par trois. La distance caractéristique entre les points est divisée par racine de trois, soit 1,732. Dans la formule de la flèche le numérateur est divisé par neuf grâce à la puissance quatrième de la longueur. On réduit donc l’écart Pic-Vallée d’un facteur neuf : C’est considérable ! Pour garder la même flèche avec le barillet augmenté, on peut réduire le dénominateur d’un facteur neuf, soit réduire l’épaisseur du verre par trois.
Donc voici déjà deux premières règles de proportion à retenir, »a rule of thumb » comme on dit outre manche.
Le nombre de points du barillet est inversement proportionnel à l’épaisseur du verre.
Pour réduire le PV d’un facteur 4, il faut multiplier par 2 les points du barillet ou multiplier par 2 l’épaisseur du verre.
Application numérique :
Pour du verre à vitre (car il plie le plus facilement que respectivement le Pyrex et le Zérodur).
Masse volumique : 2500 kg/m³ (resp. 2,23 et 2,48).
Module de Young : 60 G Pa ou 60 giga pascal (resp. 64 et 91).
Écart entre points : 0,1 m ou 10 centimètres.
Épaisseur du verre : 0,01 m ou 1 centimètre.
Soit une flèche de : 64 nm ou 64 nanomètres de verre (resp. 53 et 42 nm).
Ou bien sur l’onde : 128 nm ou Lambda sur 4,3 sur l’onde (resp. 5,2 et 6,5).
Mettons cela sous forme de formule comme une nouvelle règle approchée:
La déformation de l’onde induite par la flexion d’une poutre de verre à vitre de longueur l et d’épaisseur e, exprimées en mètres, est de :
l4/e2 fois Lambda / 4,3 sur l’onde en verre à vitre
On peut aussi retravailler la formule pour introduire la surface du verre et le nombre de points plutôt que la distance entre points. Cela donne:
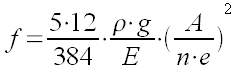
ou encore
(A / n.e)2 fois Lambda / 4,3 sur l’onde en verre à vitre
Comparaison à PLOP , Pour nos télescopes de voyage :
Dans le cas de nos télescopes de voyage : diamètre 254 mm avec 9 points(soit l=75 mm pour e=27 mm) la formule donne 2,8 nm en verre à vitre (et 2,5 nm en Pyrex !). Tandis que PLOP donne au mieux 3,6 nm PV verre. Cela semble donc proche.
Test sur un échantillon :
Toutefois la formule étant basée sur des hypothèses et approximations fortes, il faut vérifier avec un calcul PLOP sur une multitude de cas.
J’ai pris des verres de 7, 10 et 14 millimètres d’épaisseur pour obtenir des déformations sensibles; avec des barillets à 6, 9, 18 et 27 points; et avec des espacements entre points de 50 et 100 millimètres. Cela donne des verres de 276 – 340 – 480 et 586 millimètres de diamètres en 100 mm d’espacement et 138 – 170 – 240 et 293 en 50 mm.
| Déformations en nm de verre | Formule | Plop 6 pts | Plop 9 pts | Plop 18 pts | Plop 27 pts |
| Espace = 100 mm | D = 276 | D = 340 | D = 480 | D = 586 | |
| Ép. = 7,1 mm | 128 | 102 | 154 | 73 | 191 |
| Ép. = 10 mm | 64 | 50 | 75 | 37 | 74 |
| Ép. = 14 mm | 32 | 26 | 40 | 21 | 33 |
| Espace = 50 mm | D = 138 | D = 170 | D = 240 | D = 293 | |
| Ép. = 7,1 mm | 8,0 | 6,0 | 9,8 | 5,1 | 8,0 |
| Ép. = 10 mm | 4,0 | 3,4 | 5,3 | 2,9 | 4,3 |
| Ép. = 14 mm | 2,0 | 2,1 | 3,1 | 1,9 | 2,6 |
Je ne donne pas mes résultats pour 3 points: Très clairement ce sont les effets de bords qui dominent dans ce cas et la formule ne s’applique pas.
Le tableau donne pour chaque miroir le PV donné par PLOP après optimisation des positions des points supports. Pour les spécialistes de PLOP, tout ceci est sans refocalisation puisque c’est ce qui traduit bien la déformation du verre, avec un verre d’épaisseur quasi uniforme du bord au centre.
Analyse des résultats sur l'échantillon :
On retrouve avec PLOP le facteur 16 de la formule lorsque l’espacement est doublé et aussi le facteur 2 lorsque l’épaisseur est multipliée par racine de 2.
On constate des écarts de 40% en valeur. La formule n’est pas aussi rigoureuse qu’un calcul aux éléments finis. Elle ne peut pas prendre en compte les optimisations de barillet. Toutefois il n’y a pas besoin d’ajouter un coefficient d’ajustement; sans doute que les diverses approximations se compensent harmonieusement.
De toute manière pour être plus précis que 50%, il faut un calcul rigoureux. Tout cela sans compter la méconnaissance des matériaux utilisés. Ainsi PLOP utilise 60 GPa comme module d’élasticité du verre plat mais des publications donnant 66 GPa ce qui fait 10% de mieux…
Conclusion :
La formule de la barre est un outil valide. Je l’utilise maintenant depuis janvier 2006.
Formule plus rigoureuse
J’ai trouvé quelques publications Internet comme celles d’un astronome français Luc Arnold qui sont écrites en anglais (dans « Opimized axial support topologies for thin telescope mirrors » in Optical Engineering Feb 1995 Vol. 34 n°2).
Elles font référence à une équipe qui semblent avoir fondé le calcul : J.E. Nelson, J. Lubliner and T.S. Mast, « Telescope mirror supports: plate deflection on points supports » in SPIE Conf. On Advanced Technology Optical Telescopes, Proc. SPIE 332, p212-228, 1982. Ces coquins de professionnels travaillent avec notre argent mais il faut encore acheter leurs publications…
La déformation rms serait donnée par :
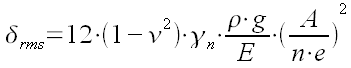
Avec des notations identiques à celles déjà utilisées ici. Mais avec en sus :
nu : le coefficient de Poisson : 0,22 pour le verre plat, 0,2 pour le Pyrex et 0,24 pour le Zérodur
gamma n : un coefficient de maillage valant 1,19.10-3 pour le triangulaire et 1,33.10-3 pour le carré.
Cette valeur de gamma est donnée dans l’hypothèse qu’il n’y a pas d’effet de bord : Convergence lorsque le nombre de points du maillage est infini. L’approximation serait de 30% avec seulement 30 points. Ce qui laisse penser que cette formule n’est peut-être pas meilleur que l’autre.
On observe que la formule est semblable : les mêmes termes apparaissent aux mêmes positions avec les mêmes puissances. Seuls sont introduits en sus le coefficient de Poisson et le paramètre de maillage mais leurs variations d’un verre à l’autre ou d’un maillage à l’autre ne sont pas très importantes.
Il reste à voir si elle recoupe les valeurs numériques de mon approximation.

Comparaison à l'approximation
Cette relation est démentie par les propres calculs de l’auteur. Il y a donc là un point troublant…
Avec une distribution gaussienne des défauts, Didier Levavasseur nous a expliqué que le rapport était de 3,375 : Lambda sur 4 en PV étant alors équivalent à Lambda sur 13,5 en rms. Dans notre cas, la taille typique des défauts est la largeur de la maille. Il n’y a pas de défaut beaucoup plus petit ni beaucoup plus grand. On constatera par la suite que ce ratio n’a pas grande importance dans la comparaison des résultats.
Test sur un échantillon :
On peut donc comparer les formules. J’ai mené la comparaison sur quatre miroirs en trois épaisseurs : Épais, mince et trop mince!
Mon 254 sur 9 points en 29, 14,5 et 7,3 mm
Le 404 de Serge sur 18 points en 36,8, 18,4 et 7,2 mm d’épaisseur
Le 820 de Vincent sur 36 points en 75,8, 37,9 et 18,95 mm d’épaisseur
Et le 1050 de Dan Bakken sur 54 points en 82,8, 41,4 et 20,7 mm
Les épaisseurs ont été choisies pour avoir la même progression de flexion de 2 à 32 nm PV (selon la formule de la barre), soit au pire Lambda sur 8 sur l’onde. Cette dernière valeur est raisonnablement au-delà de l’acceptable pour un instrument de qualité. Car il faut encore lui ajouter les défauts de la surface optique et du secondaire pour arriver au Lambda de l’instrument.
Pour les pros de PLOP, le calcul a été mené avec une obstruction centrale de 10%, sans refocalisation, sur du Pyrex et avec une épaisseur uniforme (par exemple un verre en ménisque ou un miroir de focale hyper longue). Le tableau suivant résume les résultats des différents moyens de calculs.
Pour ne pas surcharger, les résultats PLOP sont les moyennes sur les quatre miroirs. La dispersion des valeurs est d’environ 50% autour des moyennes. Cette forte dispersion ne masque pas la tendance générale. Les autres résultats sont identiques pour les quatre miroirs grâce aux choix judicieux des épaisseurs.
| Déformation en nano mètre de verre | Épais | Mince | Trop mince |
| Formule barre PV | 2,0 | 8,0 | 32 |
| Formule pro. PV | 0,77 | 3,1 | 12 |
| Formule pro. rms | 0,18 | 0,71 | 2,8 |
| Moyenne PLOP PV | 5,1 | 11 | 31 |
| Moyenne PLOP rms | 0,80 | 2,0 | 5,8 |
Analyse des résultats :
On observe que toutes les formules progressent d’un facteur quatre entre chaque épaisseur tandis que PLOP progresse d’un facteur compris entre deux et trois.
On observe que les ratios PV – rms de PLOP ne sont pas ceux de la théorie.
Enfin on observe que tandis que la formule de la barre semble bien prédire les déformations PV des miroirs les plus minces, les autres résultats semblent forts éloignés. Deux interprétations se présentent alors : Soit PLOP ne trouve pas la bonne répartition de point d’appuis (peut-être du fait des formes de barillet imposés). On pourrait donc faire de meilleurs barillets encore ! Soit les formules professionnelles donnent des valeurs asymptotiques in–atteignables du fait du peu de point des barillets retenus.
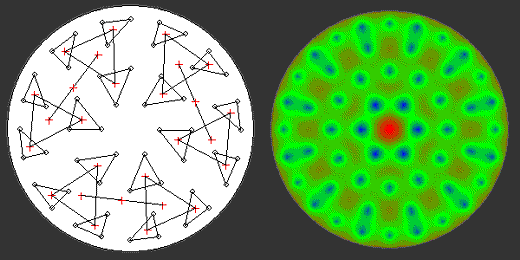
Bilan
Amusons-nous :
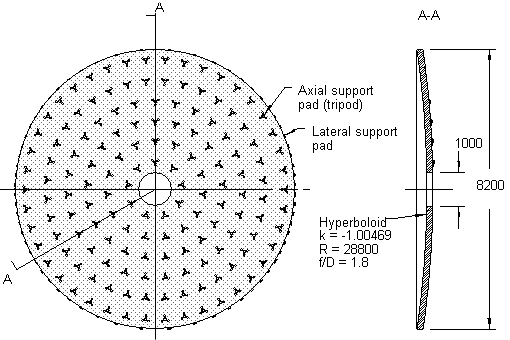
Voyons qu’elles sont les déformations induites par les supports du VLT. Nous avons:
Diamètre : 8,2 mètres Épaisseur : 0,178 mètres Matériaux : Zérodur
Vérins : 150 Points : 450
Il n’est pas évident de savoir s’il faut considérer le nombre d’appuis ou le nombre d’actionneurs. Entre les points des triangles d’appuis, le verre plie. Il y a donc une déformation sur un maillage de 450 points si les vérins épousent la bonne forme. Donc si les vérins travaillent bien on a des déformations sur 450 points. Et si les vérins travaillent mal, on couple un maillage de 150 avec un autre de 450, c’est compliqué…
Avec 450 points et la formule de la barre, on trouve : 19 nm PV verre soit Lambda sur 14 PV sur l’onde.
Avec seulement 150 vérins si tant est que l’on puisse utiliser les formules, le PV tombe à Lambda sur 1,7. C’est moins bon ! Il faut donc que les vérins marchent bien.