Observation visuelle des planètes
Introduction
Didier Levavasseur
Lors de mon premier séjour à l’observatoire du Pic de Château Renard en 1997, à la faveur d’une semaine exceptionnelle avec une turbulence systématiquement imperceptible toutes les nuits entre 0 h et 2 h TU, j’avais découvert les possibilités de mon Newton 125/720 qui, pour la première fois et la dernière d’ailleurs, me montrait la Grande Tache Rouge sur Jupiter ainsi que des détails dans les bandes équatoriales, les 2 bandes tropicales et la bande équatoriale centrale. Cela m’avait décidé à l’époque de passer à un diamètre supérieur. Mais quel instrument acheter? J’avais pu lire que, dans le domaine de l’observation planétaire, les lunettes étaient très supérieures aux télescopes à cause de leur obstruction centrale nulle. Cependant j’avais pu constater lors de cette même semaine que mon Newton n’était absolument pas ridicule face à une prestigieuse lunette apochromatique de diamètre 105 mm. Certes cette lunette donnait des images meilleures mais j’avais estimé que mon petit Newton de fabrication japonaise devait être comparable à une très bonne lunette apochromatique de 80 mm tout en restant bien meilleur marché. Il est vrai que l’argument de l’obstruction centrale liée à la présence du miroir secondaire ne m’avait jamais convaincu : l’objectif pour le planétaire n’est pas d’obtenir la meilleure résolution pour un diamètre donné mais bien la meilleure résolution pour un budget donné. Autre grande question dont les conséquences financières ne sont pas à négliger vu le coût d’un oculaire de qualité : quel grossissement utiliser et dans quelles circonstances? Il est souvent affirmé que le grossissement maximal est égal à deux fois et demi le diamètre de l’instrument exprimé en millimètres à cause de la nature ondulatoire de la lumière. Cette explication qui n’en est pas une ne m’a jamais satisfait : la lumière se comporte effectivement comme une onde mais cela n’explique en rien le fait qu’un grossissement trop élevé dégrade les images visuelles. Dernier point et non des moindres : quelle est l’influence de la qualité instrumentale et de la turbulence atmosphérique sur ces paramètres?
Comment répondre à toutes ces questions? Heureusement pour nous, l’optique physique et l’optique statistique nous fournissent un certain nombre d’outils utiles à une première approche du problème. La turbulence atmosphérique est d’ailleurs un sujet sur lequel un certain nombre d’esprits figurant parmi les plus brillants du 20ème siècle se sont penchés.
Résumé
Voici rapidement avant de nous lancer dans une étude approfondie, les grandes lignes des résultats auxquels je suis parvenu en supposant des instruments parfaitement collimatés :
- L’obstruction d’un télescope, qui est définie comme le rapport des diamètres des miroirs secondaire et primaire, n’est pas un obstacle à l’obtention d’images de qualité même si à qualité optique et diamètre égaux un instrument non obstrué donnera toujours de meilleures images.
- L’obstruction agit comme un levier sur les défauts du front d’onde, qu’ils soient d’origine instrumentale ou atmosphérique, mais elle n’est pas rédhibitoire en dessous de 33%. Un instrument pour amateur obstrué à 40% paraît en revanche plutôt orienté ciel profond tant il devient sensible à la qualité du front d’onde, notamment sur les détails de contraste moyen, par rapport à un instrument obstrué à 33%, et donc difficile à réaliser correctement. Les effets de l’obstruction sont franchement négligeables jusqu’à 20%.
- La qualité optique est le point le plus crucial. Le critère de Rayleigh dit de réflexion spéculaire, spécifiant un front d’onde de λ/13,5 rms ou λ/4 ptv, est habituellement considéré comme définissant un instrument de qualité astronomique. Ce critère n’est cependant pas suffisant pour définir un instrument performant pour l’observation planétaire, un tel instrument étant en particulier très sensible à la pente de l’erreur de front d’onde. Les instruments entre λ/20 rms (λ/6 ptv) et λ/28 rms (λ/8 ptv) sont beaucoup moins sensibles à la pente de l’erreur de front d’onde et sont idéaux pour la haute résolution : à λ/6 ptv une longueur de corrélation des défauts supérieure au dixième du diamètre est cependant préférable tandis qu’à λ/8 ptv ce paramètre n’a plus d’influence décelable. Au delà de λ/8 ptv, l’amélioration en observation planétaire n’a pas d’intérêt en regard du surcoût induit. La notion d’aberration transversale réduite n’étant pas manipulable en pratique on lui préférera celle de longueur de corrélation du front d’onde instrumental.
- A qualité du front d’onde égale et dans la gamme des diamètres inférieurs à 200 mm, il est toujours possible de trouver un instrument obstrué délivrant une image de qualité équivalente à celle d’un instrument non obstrué. Ainsi un télescope de 150 mm de diamètre à λ/20 rms pour une obstruction de 33% ne donnera jamais une image moins bonne qu’une lunette apochromatique de 105 mm supposée également à λ/20 rms, et ceci quelles que soient les conditions de turbulence atmosphérique, tout en restant meilleur marché dans un rapport 2 environ. L’intérêt des lunettes apochromatiques est à rechercher ailleurs : compacité, transportabilité, universalité, esthétique, collimation, extension et planéité du champ utilisable…
- En présence d’une turbulence atmosphérique négligeable (diamètre de Fried supérieur au diamètre de l’instrument), le grossissement optimal en observation planétaire se situe en proportion du contraste du sujet entre 1,5 et 4 fois le diamètre physique de l’instrument exprimé en millimètres, si cet instrument respecte le critère de qualité de Rayleigh précédemment évoqué. Pour un télescope obstrué à moins de 33%, on n’hésitera pas à utiliser des grossissements compris entre 1,5 et 2 fois le diamètre pour les contrastes faibles (surfaces planétaires) et jusqu’à 4 fois le diamètre pour les contrastes forts (terminateur lunaire). Tandis que pour une lunette, on poussera jusqu’à des grossissements compris entre 2 et 2,5 fois le diamètre pour les contrastes faibles et toujours jusqu’à 4 fois le diamètre pour les contrastes forts. Les grossissements doivent être adaptés aux conditions d’observation et à l’objet observé : l’utilisation de grossissements trop élevés n’apporte pas de détail supplémentaire, mais au contraire dégrade la résolution globale de l’image. Le grossissement optimal diminue bien évidemment avec le niveau de turbulence et on exploitera de manière courante le segment inférieur de la gamme de grossissement précédemment définie, soit en pratique des grossissements allant de 1 à 2 fois le diamètre de l’instrument exprimé en millimètres.
- Ces ordres de grandeur restent valables pour un instrument obstrué à 40% présentant un état de surface d’onde meilleur que λ/20 rms.
- Le grossissement optimal est celui qui harmonise, en terme de résolution c’est à dire de cycles par radians, le contenu spectral de l’image avec la réponse de l’œil. Un grossissement trop faible comme un grossissement trop élevé va positionner les plus petits détails transmis par l’instrument en dehors de la plage de résolution accessible à l’œil et ainsi fournir une image moins résolue. Lorsque l’on augmente progressivement le grossissement pour un objet donné, l’image commence par présenter des détails de plus en plus fins jusqu’à ce que l’on atteigne le grossissement optimal, puis la finesse de l’image diminue de façon relativement modérée et régulière jusqu’à ce que l’on atteigne le grossissement de coupure au delà duquel la résolution de l’image s’effondre brutalement.
- Donc l’amateur intéressé par l’observation planétaire s’orientera vers des instruments d’obstruction inférieure ou égale à 33% et présentant un état de surface d’onde de l’ordre de λ/20 rms (λ/6 ptv) à λ/28 rms (λ/8 ptv). Inutile d’investir dans une qualité optique supérieure à λ/28 rms (λ/8 ptv), l’amélioration des images planétaires ne serait pas en rapport avec l’effort financier supplémentaire consenti. Les oculaires utilisés en planétaire pourront en pratique être choisis égaux à 10/10, 15/10, et 20/10, voire pour une lunette uniquement 25/10 fois le diamètre réel de l’instrument exprimé en mm, et complétés par une lentille de Barlow x2.
- instruments limités par la diffraction
- instruments de classe professionnelle : état de surface d’onde λ/28 rms (λ/8 ptv)
- instruments de classe haute résolution : état de surface d’onde λ/20 rms (λ/6 ptv)
- instruments de classe astronomique : état de surface d’onde λ/13,5 rms (λ/4 ptv)
- instruments de classe standard : état de surface d’onde λ/10 rms (λ/3 ptv)
- un fabricant européen de lunettes apochromatiques de prestige annonce un état de surface d’onde de 30 nm rms (donc λ/20 rms à λ = 550 nm), résultat que l’on pourra étendre à tous les instruments du même type
- les fabricants russes de Maksutov annoncent une gamme standard à λ/6 ptv
- ces mêmes fabricants annoncent une gamme luxe à λ/8 ptv
- les Schmidt-Cassegrain de production de masse ne semblent jamais faire moins bien que λ/10 rms, certains particulièrement excellents affichant presque λ/30 rms
On recherchera les informations (exemple de bulletin de contrôle …sans la mesure de la longueur de corrélation) suivantes pour caractériser la qualité optique d’un instrument :
- interférogramme
- erreur de front d’onde rms
- statistique de l’erreur de front d’onde comparée à un gabarit gaussien
- longueur de corrélation de l’erreur de front d’onde
L’étude du niveau de qualité optique requis pour l’observation planétaire repose en particulier sur l’analyse de la réponse des instruments à une mire représentative d’un objet planétaire et sur le calcul du rapport de Strehl. Une simulation effectuée sur Jupiter permet de consolider les résultats obtenus.
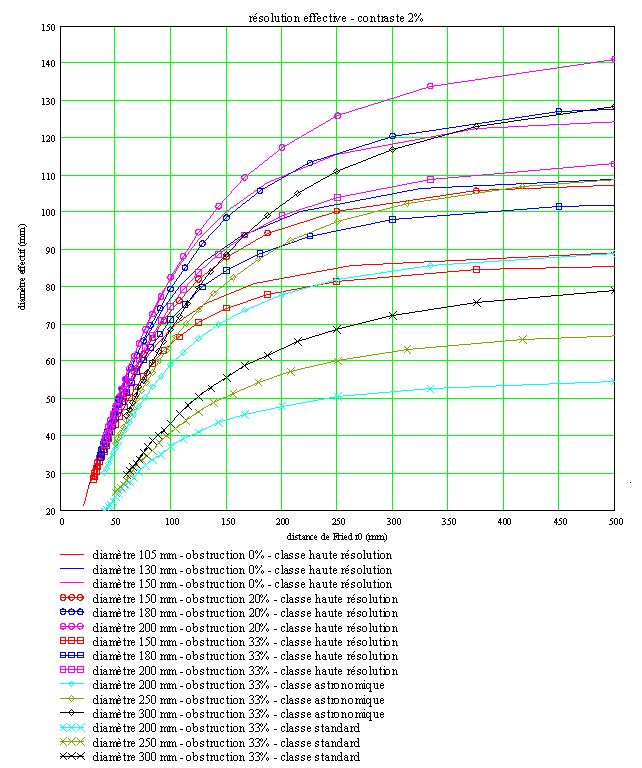
J’ai réalisé la comparaison des instruments suivants :
- lunettes de diamètres 105, 130 et 150 mm, de classe haute résolution (λ/20 rms)
- télescopes obstrués à 20% de diamètres 150, 180 et 200 mm, de classe haute résolution (λ/20 rms)
- télescopes obstrués à 33% de diamètres 150, 180 et 200 mm, de classe haute résolution (λ/20 rms)
- télescopes obstrués à 33% de diamètres 200, 250 et 300 mm, de classes astronomique (λ/13,5 rms) et standard (λ/10 rms)
La comparaison repose sur le calcul d’un diamètre effectif qui est celui de l’instrument non obstrué limité par la diffraction donnant une image équivalente. Le calcul du diamètre effectif dépend donc de l’objet observé et du capteur d’image, soit l’œil humain en ce qui nous concerne. Deux critères d’équivalence ont été appliqués sur des mires de barres sinusoïdales de contraste 2, 5 et 10% : un critère dit de résolution effective caractérisant plutôt le rendu général de l’image et un critère dit de fréquence de coupure effective caractérisant plutôt le plus petit détail perceptible. Ces deux critères donnent un classement et des ordres de grandeur comparables : le critère de résolution effective apparaît logiquement plus sévère et donne des diamètres effectifs légèrement plus faibles. J’ai retenu au final le critère de résolution effective appliqué à une mire de contraste 2% qui donne des résultats très proches de mon expérience d’observateur. Une simulation effectuée sur Jupiter permet de relier la notion de diamètre effectif à un niveau de détail obtenu sur un objet bien connu des astronomes amateurs.
Diamètre effectif et turbulence
Simulation de l'influence du diamètre effectif dans le cadre d'une observation de Jupiter



Le 02 février 2007
Bibliographie :
[R1] Edward L. O’Neill, Introduction to Statistical Optics, Addison-Wesley Publishing Company, 1963
[R2] Joseph Goodman, Statistical Optics, Wiley Interscience
[R3] F. G. Smith (Editor), Atmospheric Propagation of Radiation, The Infrared & Electro-Optical Systems Handbook Volume 2
[R4] F. Roddier, The Effects of Atmospheric Turbulence in Optical Astronomy, Progress in Optics Vol. XIX – E. Wolf (Editor), North-Holland Publishing Company (1981)
[R5] J-J Labarthe, Optique ondulatoire; Université Paris-Sud Orsay